设x∈[3,9),则∈[1,3)
∵x∈[1,3),f(x)=lnx,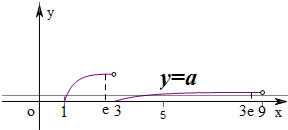
∴f()=ln,
∵函数f(x)满足f(x)=f(3x),
∴f()=f(x)=ln,
∴f(x)=,
∵在区间[1,9)内,函数g(x)=f(x)-ax有三个不同零点,
∴f(x)-ax=0在区间[1,9)上有三个解,即a=有三个解,
则y=a与h(x)=的图象有三个交点,
当x∈[1,3),h(x)==,则h′(x)==0,解得x=e,
∴当x∈[1,e)时,h′(x)>0,当x∈(e,3)时,h′(x)<0即函数h(x)==在[1,e)上单调递增,在(e,3)上单调递减,
∴当x=e处,函数h(x)==在[1,3)上取最大值,
当x∈[3,9),h(x)==,则h′(x)==0,解得x=3e,
∴当x∈[3,3e)时,h′(x)>0,当x∈(3e,9)时,h′(x)<0即函数h(x)==在[3,3e)上单调递增,在(3e,9)上单调递减,
∴当x=3e处,函数h(x)==在[3,9)上取最大值,
根据函数的单调性,以及h(1)=0,h(e)=,h(3)=0,h(3e)=,h(9)=,画出函数的大值图象,
根据图象可知y=a与h(x)在[1,3)上一个交点,在[3,3e) 上两个交点,
∴在区间[1,9)内,函数g(x)=f(x)-ax有三个不同零点,则实数a的取值范围是(,).
故选:B.

