问题
解答题
若函数f(x)=ax3-bx+4,当x=2时,函数f(x)有极值为-
(Ⅰ)求函数f(x)的解析式; (Ⅱ)若f(x)=k有3个解,求实数k的取值范围. |
答案
(Ⅰ)f′(x)=3ax2-b
由题意;
,解得f′(2)=12a-b f(2)=8a-2b+4=- 4 3
,a= 1 3 b=4
∴所求的解析式为f(x)=
x3-4x+41 3
(Ⅱ)由(1)可得f′(x)=x2-4=(x-2)(x+2)
令f′(x)=0,得x=2或x=-2,
∴当x<-2时,f′(x)>0,当-2<x<2时,f′(x)<0,当x>2时,f′(x)>0
因此,当x=-2时,f(x)有极大值
,28 3
当x=2时,f(x)有极小值-
,4 3
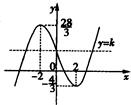
∴函数f(x)=
x3-4x+4的图象大致如图.1 3
由图可知:-
<k<4 3
.28 3