问题
选择题
如图所示，长为2L的轻杆，两端各固定一小球，A球质量为
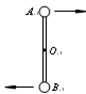
，B球质量为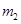
，过杆的中点O有一水平光滑固定轴，杆可绕轴在竖直平面内转动。当转动到竖直位置且A球在上端，B球在下端时杆的角速度为ω，此时杆对转轴的作用力为零，则A、B两小球的质量之比为（ ）
A．1：1 B．(Lω2+2g): (Lω2-2g)
C．(Lω2-g): (Lω2+g) D．(Lω2+g): (Lω2-g)
答案
答案：D
对整体受力分析得：整体受到向下的A球、B球重力，B球的离心力整体受到向上的A球的离心力则：v="ωL" m1v2/L=m1g+m2g+m2v2/L 即m1ω2L=m1g+m2g+m2ω2L m1(ω2L-g)=m2(g+ω2L) 所以m1：m2=(g+ω2L)/(ω2L-g)。D正确。故本题选D。