问题
问答题
（1）该星球表面的重力加速度g
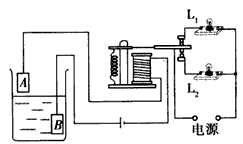
（2）若在该星球表面有一如图所示的装置，其中AB部分为一长为12.8m并以5m/s速度顺时针匀速转动的传送带，BCD部分为一半径为1.6m竖直放置的光滑半圆形轨道，直径BD恰好竖直，并与传送带相切于B点。现将一质量为0.1kg的可视为质点的小滑块无初速地放在传送带的左端A点上，已知滑块与传送带间的动摩擦因数为0.5。问：
滑块能否到达D点？若能到达，试求出到达D点时对轨道的压力大小；若不能到达D点，试求出滑块能到达的最大高度及到达最大高度时对轨道的压力大小。
答案
（1）1.6 m/s2（2）0.48 N
（1）对距星球表面h=R处的卫星（设其质量为m），有：
① （2分）
对在星球表面的物体m′，有：
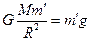② （2分）
解得：g = 1.6 m/s2 （2分）
（2）设滑块从A到B一直被加速，且设到达B点时的速度为VB
则：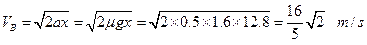
（2分）
因VB < 5m/s，故滑块一直被加速 （1分）
设滑块能到达D点，且设到达D点时的速度为VD
则在B到D的过程中，由动能定理：–mg·2R = 
mVD2–mVB2 （2分）
解得：
（2分）
而滑块能到达D点的临界速度：V0 =
=" 1.6" m/s < VD，即滑块能到达D点。
（1分）
在D点取滑块为研究对象，则有： FN + mg = 
（2分）
解得：FN = – mg = 0.1×3.22/1.6 – 0.1×1.6 =" 0.48" N （2分）
