设正四面体S-ABCD如图所示，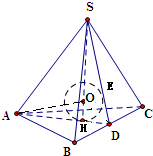

可得它的内切球的球心0必定在高线SH上

延长AH交BC于点D，则D为BC的中点，连结SD则内切球切SD于点E，连结AO

∵H是正三角形ABC的中心

∴AH：HD=2：1

∵Rt△0AH∽Rt△DSH

∴

OA

OH

=

DS

DH

=3，可得OA=30H=S0

因此，SH=4OH，可得内切球的半径OH=

1

4

SH

∵正四面体棱长为1

∴Rt△SHD中，SD=

3

2

，HD=

1

3

SD=

3

6

可得SH=

SD2-HD2

=

6

3

，得内切球的半径r=OH=

1

4

×

6

3

=

6

12

因此正四面体内切球的表面积为S=4πr²=

π

6

故选：A