问题
解答题
已知函数f(x)=x3+ax2+bx+c，过曲线y=f(x)上的点P(1，f(1))的切线方程为y=3x+1．
(Ⅰ)若函数f(x)在x=－2处有极值，求f(x)的表达式；
(Ⅱ)若函数y=f(x)在区间[－2,1]上单调递增，求实数b的取值范围．
答案
（1）f(x)=x3+2x2－4x+5（2）b≥0
(Ⅰ )由f(x)=x3+ax2+bx+c，求导数得f′(x)=3x2+2ax+b．
过y=f(x)上的点P(1，f(1))的切线方程为：y－f(1)=f′(1)(x－1)，
即y－(a+b+c+1)=(3+2a+b)(x－1)．
而过y=f(x)上的点P(1，f(1)) 的切线方程为y=3x+1，
故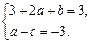
即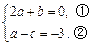
∵f(x)在x=－2处有极值，故f′(－2)=0，∴－4a+b=－12，③
由①②③得a=2，b=－4，c=5．
∴f(x)=x3+2x2－4x+5．
(Ⅱ )解：y=f(x)在[－2,1]上单调递增，又f′(x)=3x2+2ax+b，由①知2a+b=0．
依题意f′(x)在[－2,1]上恒有f′(x)≥0，即3x2－bx+b≥0．
，可得b(x－1)≤3x2．
当x=1时，不等式显然成立．
当x≠1时，x－1<0，∴b≥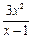
．
∵
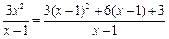=3(x－1)+
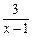+6≤－6+6="0 " ∴b≥0