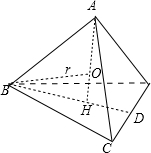
如图所示：设正四面体的棱长等于a，球的半径等于r，作AH垂直于平面BCD，H为垂足．

则BH=

2

3

•BD=

2

3

•

3

2

a=

3

3

a，故AH=

AB2-BH2

=

a2-( 3 a 3 )2

=

6

3

a．

再由AH=4，可得

6

3

a=4，∴a=

12

6

．

Rt△BOH中，由勾股定理可得 r2=(4-r)2+(

3

3

a)2，解得r=3．

故球的表面积为4πr²=36π，

故选C．