问题
解答题
(1)解不等式
(2)a,b∈R+,2c>a+b,求证c-
|
答案
(1)原不等式等价于
≥0,即-x2+2x+8 x2-2x-3
≤0,(x-4)(x+2) (x-3)(x+1)
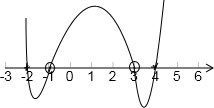
由穿根法(并验根)求得 x∈[-2,-1)∪(3,4].
(2)要证原式成立,即证-
<a<c<c2-ab
,即证|a-c|<c2-ab
,即证|a-c|2<(c2-ab
)2,c2-ab
即证a2-2ac+c2<c2-ab,即证a2+ab>2ac,即证a+b<2c,由题设,此式成立,
∴原命题成立.
