问题
解答题
求证:等腰三角形两底角的平分线相等.
答案
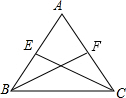
已知:△ABC中,AB=AC,BF,CE分别∠ABC,∠ACB的角平分线.
求证:BF=CE,即等腰三角形的两底角的平分线相等
证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BF,CE分别∠ABC,∠ACB的角平分线,
∴∠BCE=∠CBF,
∵∠ABC=∠ACB,BC=BC,
∴△BCE≌△CBF,
∴BF=CE,即等腰三角形两底角的平分线相等.
求证:等腰三角形两底角的平分线相等.

已知:△ABC中,AB=AC,BF,CE分别∠ABC,∠ACB的角平分线.
求证:BF=CE,即等腰三角形的两底角的平分线相等
证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BF,CE分别∠ABC,∠ACB的角平分线,
∴∠BCE=∠CBF,
∵∠ABC=∠ACB,BC=BC,
∴△BCE≌△CBF,
∴BF=CE,即等腰三角形两底角的平分线相等.