问题
填空题
设点A（x1，f（x1）），B（x2，f（x2）），T（x0，f（x0））在函数f（x）=x3-ax（a＞0）的图象上，其中x1，x2是f（x）的两个极值点，x0（x0≠0）是f（x）的一个零点，若函数f（x）的图象在T处的切线与直线AB垂直，则a=______．
答案
令f（x）=0，（a＞0），则x(x+
)(x-a
)=0，解得x=0，±a
．a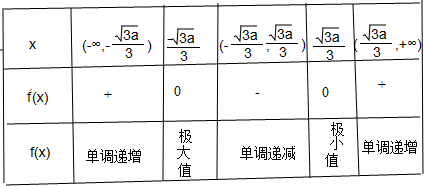 
∵x0（x0≠0）是f（x）的一个零点，∴x0=-
或x0=a
．a
∵f′（x）=3x2-a=3(x+
)(x-3a 3
)，3a 3
令f′（x）=0，解得x=±
，列表如下：3a 3
由表格可知：当x=
时，函数f（x）取得极小值，且f(3a 3
)=-3a 3
；2a 3a 9
当x=-
时，函数f（x）取得极大值，且f(-3a 3
)=3a 3
；2a 3a 9
不妨设A(-
，3a 3
)，B(2a 3a 9
，-3a 3
)．∴KAB=2a 3a 9
．-2a 3
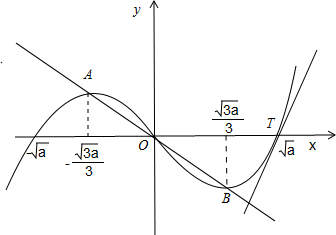根据表格作出如下图象：
①当x0=
时．f′(a
)=2a，a
∵函数f（x）的图象在T处的切线与直线AB垂直，
∴-
×2a=-1，（a＞0），解得a=2a 3
．3 2
②当x0=-
时．f′(a
)=2a，a
∵函数f（x）的图象在T处的切线与直线AB垂直，
∴-
×2a=-1，（a＞0），解得a=2a 3
．3 2
综上可知：满足条件的a的值为
．3 2
故答案为
．3 2