问题
解答题
求证:等腰三角形两腰上的高的交点到底边两端的距离相等.
答案
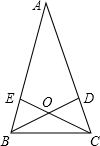
已知:△ABC中AB=AC,CE⊥AB,BD⊥AC,交点为O,
求证:OB=OC.
证明:∵AB=AC,
∴∠ABC=∠ACB.
∵CE⊥AB,BD⊥AC,
∴∠CEB=∠BDC=90°.
∵BC=CB,
∴△CBE≌△BCD.
∴∠ECB=∠DBC.
∴OB=OC.
即等腰三角形两腰上的高的交点到底边两端的距离相等.
求证:等腰三角形两腰上的高的交点到底边两端的距离相等.

已知:△ABC中AB=AC,CE⊥AB,BD⊥AC,交点为O,
求证:OB=OC.
证明:∵AB=AC,
∴∠ABC=∠ACB.
∵CE⊥AB,BD⊥AC,
∴∠CEB=∠BDC=90°.
∵BC=CB,
∴△CBE≌△BCD.
∴∠ECB=∠DBC.
∴OB=OC.
即等腰三角形两腰上的高的交点到底边两端的距离相等.