问题
计算题
用长L1=4m和长为L2=3m的两根细线,拴一质量m=2kg的小球A,L1和L2的另两端点分别系在一竖直杆的O1,O2处,已知O1O2=5m如下图(g=10m·s-2)
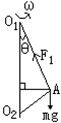
(1)当竖直杆以的角速度ω匀速转动时,O2A线刚好伸直且不受拉力.求此时角速度ω1.
(2)当O1A线所受力为100N时,求此时的角速度ω2.
答案
略
(1)当O2A线刚伸直而不受力时,受力如图所示。
则F1cosθ="mg" ①
F1sinθ="mRω12" ②
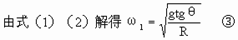
由几何知识知
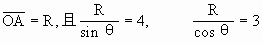
∴R="2.4m" θ=37°
代入式③ω1=1.77(rad/s)
(2)当O1A受力为100N时,由(1)式
F1cosθ=100×0.8= 80(N)>mg
80(N)>mg
由此知O2A受拉力F2。则对A受力分析得
F1cosθ-F2sinθ-mg="0" ④
F1sinθ+F2cosθ=" mRω22" ⑤
由式(4)(5)得

