问题
填空题
已知f(x)=x3+3ax2+bx+a2(a>1)在x=-1处有极值0,则a+b=______.
答案
∵函数f(x)=x3+3ax2+bx+a2
∴f'(x)=3x2+6ax+b,
又∵函数f(x)=x3+ax2+bx+a2在x=-1处有极值0,
∴
,∴3-6a+b=0 -1+3a-b+a2=0
或a=1 b=3 a=2 b=9
当
时,f'(x)=3x2+6ax+b=3(x+1)2=0,方程有两个相等的实数根,不满足题意;a=1 b=3
当
时,f'(x)=3x2+6ax+b=3(x+1)(x+3)=0,方程有两个不等的实数根,满足题意;a=2 b=9
∴a+b=11
故答案为:11.

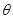 的光滑绝缘斜面处于水平向右的匀强电场中.一电荷量为+q、质量为m的小球,以初速度v0由斜面底端的M点沿斜面上滑,到达斜面顶端N的速度仍为v0.则
的光滑绝缘斜面处于水平向右的匀强电场中.一电荷量为+q、质量为m的小球,以初速度v0由斜面底端的M点沿斜面上滑,到达斜面顶端N的速度仍为v0.则