问题
选择题
若函数f（x）=x3-6bx+3b在（0，1）内只有极小值，则实数b的取值范围是（ ）
|
答案
∵f′（x）=3x2-6b，由题意，函数f′（x）图象如右．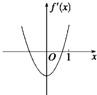
∴f′(0)＜0 f′(1)＞0
即-6b＜0 3-6b＞0
得0＜b＜
．1 2
故选D
搜题请搜索小程序“爱下问搜题”
若函数f（x）=x3-6bx+3b在（0，1）内只有极小值，则实数b的取值范围是（ ）
|
∵f′（x）=3x2-6b，由题意，函数f′（x）图象如右．
∴f′(0)＜0 f′(1)＞0
即-6b＜0 3-6b＞0
得0＜b＜
．1 2
故选D