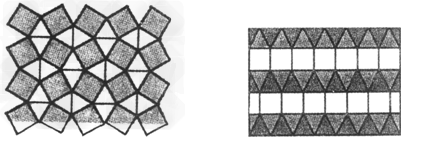
问题
解答题
在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌),这显然与正多边形的内角大小有关,当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成一个平面图形。
(1)请根据下列图形,填写表中空格:


(2)如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
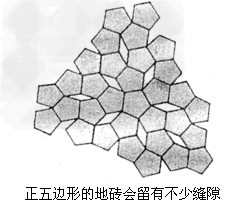
(3)不能用正五边形形状的材料铺满地面的理由是什么?
(4)某家庭准备用正三角形与正六边形两种瓷砖结合在一起镶嵌地面,由你帮助设计镶嵌图案,你能设计几种不同的镶嵌方案?
(5)正三角形和正方形组合呢?(画图说明)
答案
解:(1)

(2)正三角形、正方形、正六边形;
(3)因为正五边形的每一个内角是108°,它不是360°的约数,所以不行,
同理,因为正七边形、正八边形等的每一个内角,也分别不是360°的约数,所以也都不行;
(4)参考图案:

(5)参考图案: