问题
填空题
方程x3-3x+a+1=0在x∈[-2,+∞)上有三个不同的实根,则实数a的取值范围为______.
答案
f(x)=x3-3x+a+1,f'(x)=3x2-3=3(x+1)(x-1),
当x∈(-∞,-1),f'(x)>0;
x∈(-1,1),f'(x)<0;
x∈(1,+∞),f'(x)>0.
∴f(x)在x=-1取极大值3+a,在x=1时取极小值a-1.
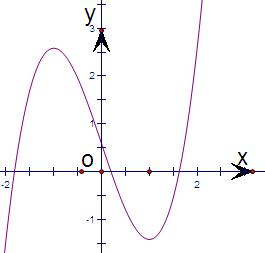
根据f(x)的大致图象的变化情况,有三个不同的实数解时,
f(-1)>0 f(1)<0 f(-2)<0
解得a的取值范围是-3<a<1.
故答案为:-3<a<1.