（1）对函数f（x）求导，f′(x)=

4

3

•

1-x2

(x2+1)2

．

令f'（x）=0得x=1或x=-1．

当x∈（0，1）时，f'（x）＞0，f（x）在（0，1）上单调递增；

当x∈（1，2）时，f'（x）＜0，f（x）在（1，2）上单调递减．

又f(0)=0，f(1)=

2

3

，f(2)=

8

15

，

所以当x∈[0，2]，f（x）的值域是[0，

2

3

]；

（2）设函数g（x）在[0，2]上的值域是A．

∵对任意x₁∈[0，2]，总存在x₀∈[0，2]，使f（x₁）-g（x₀）=0，

∴[0，

2

3

]⊆A．

对函数g（x）求导，g'（x）=ax²-a²．

①当a＜0时，若x∈（0，2），g'（x）＜0，所以函数g（x）在（0，2）上单调递减．

∵g(0)=0，g(2)=

8

3

a-2a2＜0，

∴当x∈[0，2]时，不满足[0，

2

3

]⊆A；

②当a＞0时，g′(x)=a(x-

a

)(x+

a

)．

令g'（x）=0，得x=

a

或x=-

a

（舍去）．

（i）当x∈[0，2]，0＜

a

＜2时，列表：

∵g(0)=0，g(

a

)＜0，

又∵[0，

2

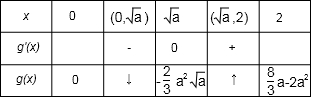
3

]⊆A，∴g(2)=

8

3

a-2a2≥

2

3

，解得

1

3

≤a≤1．

（ii）当x∈（0，2），

a

≥2时，g'（x）＜0，∴函数在（0，2）上单调递减，

∵g（0）=0，∴g(2)=

8

3

a-2a2＜0∴当x∈[0，2]时，不满足[0，

2

3

]⊆A．

综上，实数a的取值范围是[

1

3

，1]．