问题
计算题
如图所示，是某公园设计的一种惊险刺激的娱乐设施，轨道CD部分粗糙，μ=0.1，其余均光滑。第一个圆管轨道的半径R=4m，第二个圆管轨道的半径r=3.6m。一挑战者质量m=60kg，沿斜面轨道滑下，滑入第一个圆管形轨道（假设转折处无能量损失），挑战者到达A、B两处最高点时刚好对管壁无压力，然后从平台上飞入水池内，水面离轨道的距离h=1m。g取10 m/s2，管的内径及人相对圆管轨道的半径可以忽略不计。则：
小题1:挑战者若能完成上述过程，则他应从离水平轨道多高的地方开始下滑?
小题2:CD部分的长度是多少?
小题3:挑战者入水时的方向(用与水平方向夹角的正切值表示)?
答案
小题1:10米
小题2:10米
小题3:与水平方向成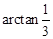
解答：解：小题1:在A点无压力则 mg=m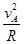
,根据机械能守恒有，
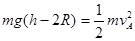，解得h=10m
所以挑战者应从离水平轨道10m的地方开始下滑
小题2:在B点无压力则mg=m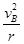
,
由A到B动能定理得， mg（2R-2r）-fL=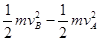
，
，
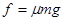联立方程得 ，CD部分的长度L=10m
小题3:由B到D过程中，根据动能定理可得，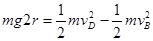
，解得
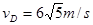，挑战者从平台飞出，做平抛运动，竖直速度
，
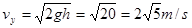设挑战者入水时的方向与水平方向的夹角为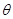
，则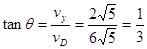
，则落水时速度方向与水平方向成