问题
计算题
如图所示,一个质量为m=0.6kg的小球,在左侧平台上运行一段距离后从边缘A点以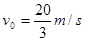 水平飞出,恰能沿切线从P点进入竖直圆弧管道并继续滑行。已知管道口径远小于圆弧半径,OP与竖直方向的夹角是37°,平台到地面的高度差为h=1.45m。若小球运动到圆弧轨道最低点时的速度大小是 10m/s。取g=10m/s2,sin53°=0.8,cos53°=0.6。求:
水平飞出,恰能沿切线从P点进入竖直圆弧管道并继续滑行。已知管道口径远小于圆弧半径,OP与竖直方向的夹角是37°,平台到地面的高度差为h=1.45m。若小球运动到圆弧轨道最低点时的速度大小是 10m/s。取g=10m/s2,sin53°=0.8,cos53°=0.6。求:
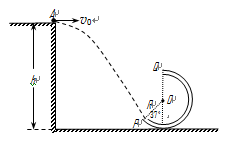
(1)P点距地面的高度
(2)圆弧轨道最低点对小球支持力的大小
(3)若通过最高点Q点时小球对外管壁的压力大小9N,则小球经过Q点时的速度大小是多少?
答案
(1) 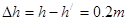 (2) 66N(3) v2=5m/s
(2) 66N(3) v2=5m/s
(1)对P点的速度矢量分解,有:
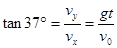 (2分)
(2分) 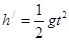 (2分)
(2分)
带入数据得:t=0.5s 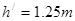
所以P点距地面的高度为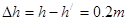 (1分)
(1分)
(2)做小球在最低点的受力分析可知:
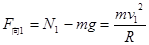 (2分)
(2分)
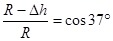 (1分)
(1分)
带入数据得:R=1m N1=66N
再由牛顿第三定律N / = N1="66N" (1分)
(3)对小球在最高点进行受力分析:
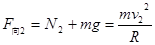 (2分)
(2分)
带入数据得:v2=5m/s (1分)
