问题
填空题
已知球面上两点A,B之间的球面距离为4π,过这两点的两条球半径之间的夹角为60°,以AB为直径的球的小圆的面积为______.
答案
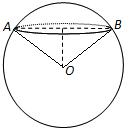
设球心为O,
∵两点A,B之间的球面距离为4π,过这两点的两条球半径之间的夹角为60°,
∴4π=
×OA,∴OA=12,π 3
在△AOB中,球O的小圆直径AB,球O的半径长为12,∠AOB=60°.
解得AB=12,
所以以AB为直径的球的小圆的面积为(
) 2 π=36π,12 2
故答案为:36π.
