问题
选择题
如图所示，圆锥摆甲乙的摆长之比为2:1，两摆球的质量相同，今使两圆锥摆做顶角分别为30°、60°的圆锥摆运动，则（ ）
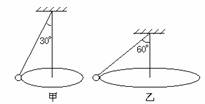
A．两摆球的向心加速度之比为1:3
B．两圆锥摆的运动周期之比为2:1
C．摆球的线速度之比为1:1
D．摆球的角速度之比为1:2
答案
答案：A
考点：
专题：牛顿第二定律在圆周运动中的应用．
分析：小球在水平面内做匀速圆周运动，对小球受力分析，根据向心力基本公式即可解题．
解答：解；解：小球在水平面内做匀速圆周运动，对小球受力分析，如图
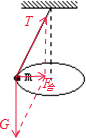
设细线与竖直方向的夹角为θ，r=Lsinθ，F合=mgtanθ，L1=2L2
根据牛顿第二定律得：a=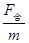
=gtanθ，所以两摆球的向心加速度之比为
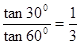，故A正确；
根据向心加速度公式a=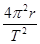
得：T=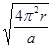
，所以两圆锥摆的运动周期之比为
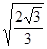，故B错误；
根据向心力公式F合=m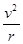
得：摆球的线速度之比为
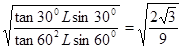，故C错误；
根据角速度与周期的关系ω=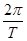
得：摆球的角速度之比为
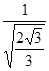，，故D错误．
故选A．
点评：本题主要考查了向心力基本公式的直接应用，要求同学们能根据几何关系求出物理量之间的关系，难度适中．