设函数f(x)=x+ax2+blnx,曲线y=f(x)过点P(1,0),且在点P处的切线斜率为2.
(Ⅰ)求a,b的值;
(Ⅱ)求f(x)的极值点;
(Ⅲ)对定义域内任意一个x,不等式f(x)≤2x-2是否恒成立,若成立,请证明;若不成立,请说明理由.
(Ⅰ)∵f(x)=x+ax2+blnx(x>0)
∴f′(x)=1+2ax+
,b x
∵y=f(x)在点P(1,0)处的切线斜率为2,
∴
即f(1)=0 f′(1)=2 1+a=0 1+2a+b=2
解得
,a=-1 b=3
∴a=-1,b=3.
(Ⅱ)∵f(x)=x-x2+3lnx(x>0)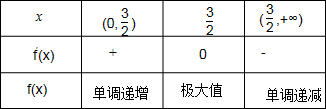
得f′(x)=1-2x+
=3 x
,-2x2+x+3 x
即f′(x)=(-2x+3)(x+1) x
由x>0可得,
当f'(x)>0时,解得0<x<
,3 2
当f'(x)<0时,解得x>
.3 2
列表可得:
故f(x)只有极大值点,且极大值点为x=
.3 2
(Ⅲ)令g(x)=f(x)-2x+2,得g(x)=-x2-x+2+3lnx(x>0),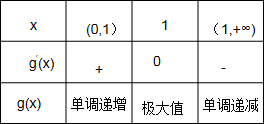
∴g′(x)=-2x-1+
=3 x
,-2x2-x+3 x
即g′(x)=
.(2x+3)(-x+1) x
由x>0可得,
当g'(x)>0时,解得0<x<1;
当g'(x)<0时,x>1.
列表可得:
由表可知g(x)的最大值为g(1)=0.
即g(x)≤0恒成立,因此f(x)≤2x-2恒成立.

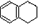 ,分子式是C10H12.常温下为无色液体,有刺激性气味,沸点207℃,不溶于水,是一种优良的溶剂,它与液溴发生反应:C10H12+4Br2→C10H8Br4+4HBr.生成的四溴化萘常温下为固态,不溶于水,有人用四氢化萘、液溴、蒸馏水和纯铁粉为原料,制备少量饱和氢溴酸溶液,实验步骤如下:
,分子式是C10H12.常温下为无色液体,有刺激性气味,沸点207℃,不溶于水,是一种优良的溶剂,它与液溴发生反应:C10H12+4Br2→C10H8Br4+4HBr.生成的四溴化萘常温下为固态,不溶于水,有人用四氢化萘、液溴、蒸馏水和纯铁粉为原料,制备少量饱和氢溴酸溶液,实验步骤如下: