（1）函数的导数f'（x）=3x²+2f'（1），令x=1得，f'（1）=3+2f'（1），解得f'（1）=-3．

所以f(x)=x3-6x，f′(x)=3x2-6x=3(x-

2

)(x+

2

)．

列表：当x变化时，f'（x），f（x）的变化情况如下表：

x	-3	（-3，- 2 ）	- 2	（- 2 ， 2 ）	2	（ 2 ，3）	3
f'（x）		+		-		+
f（x）	-9	递增	4 2	递减	-4 2	递增	9

所以当x=-

2

时，取得极大值f（x）=4

2

，当x=

2

时，取得极小值f（x）=-4

2

．

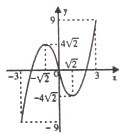
（2）由（1）可以作出函数f（x）=x³-6x在[-3，3]上的大致图象如图：

当m∈（-∞，-9）∪（9，+∞）时，方程无实数根；

当m∈[-9，-4

2

）∪（4

2

，9]时，方程有一个实数根；

当m=-4

2

或m=4

2

时，方程有两个不等的实数根；

当m∈（-4

2

，4

2

）时，方程有三个不等的实数根．