问题
解答题
| 已知函数f(x)=x3+ax2+bx+c在x=1处的切线方程为y=3x+1, (1)若函数y=f(x)在x=-2时有极值,求f(x)的表达式; (2)在(1)条件下,若函数y=f(x)在[-2,m]上的值域为[
(3)若函数y=f(x)在区间[-2,1]上单调递增,求b的取值范围. |
答案
(1)f′(x)=3x2+2ax+b
∵曲线y=f(x)在点P(1,f(1))处的切线方程为y=3x+1.
∴
即 f′(1)=3 f(1)=4 3+2a+b=3 1+a+b+c=4
∵函数y=f(x)在x=-2时有极值
∴f′(-2)=0即-4a+b=-12
∴3+2a+b=3 1+a+b+c=4 -4a+b=-12 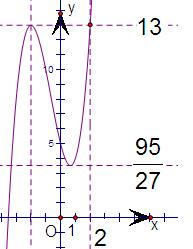
解得a=2,b=-4,c=5
∴f(x)=x3+2x2-4x+5
(2)由(1)得:f(x)=x3+2x2-4x+5,画出它的图象,如图,
由图可知,
若函数y=f(x)在[-2,m]上的值域为[
,13],95 27
m的取值范围是:[
,2].5 3
(3)由(1)知,2a+b=0
∴f′(x)=3x2-bx+b
∵函数y=f(x)在区间[-2,1]上单调递增
∴f′(x)≥0即3x2-bx+b≥0在[-2,1]上恒成立
①当x=
≥1时f′(x)的最小值为f′(1)=1-b+b≥0∴b≥6b 6
②当x=
≤-2时,f′(x)的最小值为f′(-2)=12+2b+b≥0∴b∈∅b 6
③-2<
<1时,f′(x)的最小值为 b 6
≥0∴0≤b≤612b-b2 12
总之b的取值范围是b≥0
