问题
填空题
已知实数a≠0,函数f(x)=ax(x－2)2(x∈R)有极大值32,则实数a等于______.
答案
27
本题考查函数的极值.可导函数极值点处的导数为0.
f(x)=ax(x2－4x＋4)=ax3－4ax2＋4ax,
∴f′(x)=3ax2－8ax＋4a=a(3x2－8x＋4)=a(3x－2)(x－2).
令f′(x)=0,得x1=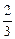
或x2=2.
∴在x1=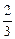或x2=2处取得极值.把x=2代入验证,极值为0,
因此函数在x=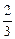处取得极值32,即a×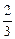×(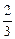－2)2=32.
解得a=27.