问题
填空题
已知f(x)=sin(ωx+
|
答案
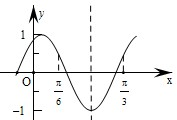
如图所示,
∵f(x)=sin(ωx+
),π 3
且f(
)=f(π 6
),π 3
又f(x)在区间(
,π 6
)内只有最小值、无最大值,π 3
∴f(x)在
=
+π 6 π 3 2
处取得最小值.π 4
∴
ω+π 4
=2kπ-π 3
(k∈Z).π 2
∴ω=8k-
(k∈Z).10 3
∵ω>0,
∴当k=1时,ω=8-
=10 3
;14 3
当k=2时,ω=16-
=10 3
,此时在区间(38 3
,π 6
)内已存在最大值.π 3
故ω=
.14 3
故答案为:14 3