问题
填空题
已知A,B,C三点在球心为O,半径为R的球面上,AC⊥BC,且AB=R,那么A,B两点的球面距离为______,球心到平面ABC的距离为______.
答案
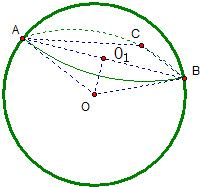
如图,因为AC⊥BC,所以AB是截面的直径,
又AB=R,所以△OAB是等边三角形,
所以DAOB=
,故A,B两点的球面距离为π 3
R,π 3
于是DO1OA=30°,所以球心到平面ABC的距离
OO1=Rcos30°=
R.3 2
故答案为:
R;π 3
.
R3 2
