问题
填空题
已知点A、B在平面α的同侧,且到平面α的距离分别为d与3d,则A、B的中点到平面α的距离为______.
答案
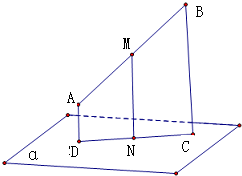
分别作AD⊥α于D,BC⊥α于C,连接DC
再分别取AB、DC中点M、N,连接MN
∵AD⊥α,BC⊥α
∴AD∥BC
可得MN是梯形ABCD的中位线
∴MN=
(AD+BC)1 2
∵AD⊥α,BC⊥α
∴NM∥BC∥AD,MN是AB中点到平面α的距离
且AD、BC分别为点A、B到平面α的距离
即AD=d,BC=3d
∴MN=
(AD+BC)=2d1 2
故答案为:2d
