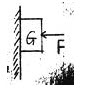
如图所示,一个质量为m的小孩在平台上以加速度a做匀加速助跑,目的是抓住在平台右端的、上端固定的、长度为L的轻质悬绳,并在竖直面内做圆周运动.已知轻质绳的下端与小孩的重心在同一高度,小孩抓住绳的瞬间重心的高度不变,且无能量损失.若小孩能完成圆周运动,则:
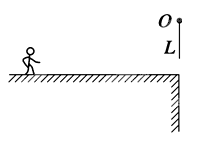
(1) 小孩抓住绳的瞬间对悬线的拉力至少为多大?
(2) 小孩的最小助跑位移多大?
（3）设小孩在加速过程中，脚与地面不打滑，求地面对脚的摩擦力大小以及摩擦力对小孩所做的功。
（1）F=6mg，v12=5gL。（2）x=
=
（3）地面对小孩的摩擦力位移为零，摩擦力对小孩做功为零
解：(1)小孩能完成竖直面内的圆周运动，则在最高点最小的向心力等于小孩所受的重力。设小孩在竖直面内最高点运动的速度为v2.，依据牛顿第二定律小孩在最高点有: mg=m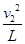
… ………………………………………2分
设小孩在最低点运动的速度为v1，小孩抓住悬线时悬线对小孩的拉力至少为F，
依据牛顿第二定律小孩在最低点有：F—mg=m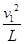
… ………………………………2分
小孩在竖直面内做圆周运动，依据机械能守恒定律可得，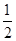 
mv22+2mgL=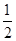mv12………2分
联立以上三式解得：F=6mg，v12=5gL。… ……………………………2分
依据牛顿第三定律可知,小孩对悬线的拉力至少为6mg。… …………………………1分
(2)小孩在水平面上做初速度为零的匀加速直线运动，根据题意，小孩运动的加速度为a，末速度为v1,，根据匀变速直线运动规律，v12=2ax… …………………………2分
解得：x==… ………………………………………2分
（3）由牛顿运动定律可知摩擦力大小f="ma" … ………………………2分
由于地面对小孩的摩擦力位移为零，所以摩擦力对小孩做功为零。………………………3分