问题
解答题
已知函数f(x)=x|x2-a| （a∈R）,
(1)当a≤0时，求证函数f(x)在（-∞，+∞）上是增函数；
（2）当a=3时，求函数f(x)在区间［0，b］上的最大值
答案
（1）证明如下 （2）f(x)max=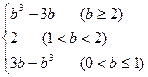
（1）a≤0 f(x)=x(x2-a)=x3-ax
∴f′(x)=3x2-a≥0，f(x)在（-∞，+∞）上为增函数
（2）a=3时f(x)=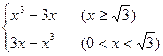
①若0<b≤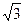
时，f(x)=3x-x3
由f′(x)=3-3x2="0"
得x=1
(Ⅰ)若0<b≤1时f′(x) ≥0，f(x)在[0,b]上递增，
故f(x)max=f(b)=3b-b3
(Ⅱ)若1<b≤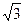时，0<x<1,②f′(x)>0; 1<x<b, f′(x)<0
故f(x)max=f(1)=2②若b>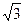由①知f(x)在[0, 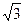]上最大值为2，下面求f(x)在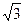（,b]上的最大值
∵f′(x)=3x2-3>0 ∴f(x)max=f(b)=b3-3b
又b3-3b-2=(b+1)2(b-2)
∴f(x)max=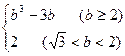
综合①已知f(x)max=