已知向量
(1)求ω; (2)若x∈(0,
(3)若cosx≥
|
由题意,f(x)=
sinωx•cosωx-cos2ωx+3 1 2
=
sin2ωx-3 2
+1+cos2ωx 2 1 2
=
sin2ωx-3 2
cos2ωx1 2
.=sin(2ωx-
)π 6
(1)∵两相邻对称轴间的距离为
∴T=π 4
=2π 2ω
,∴ω=2π 2
(2)由(1)知f(x)=sin(4x-
),令2kπ-π 6
≤4x-π 2
≤2kπ+π 6
,k∈z,解得π 2
-kπ 2
≤x≤π 12
+kπ 2
,k∈z又x∈(0,π 6
π),故函数的单调递增区间是(0,5 12
)π 6
(3)∵cosx≥
,又因为余弦函数在(0,π)上是减函数,∴x∈(0,1 2
]π 3
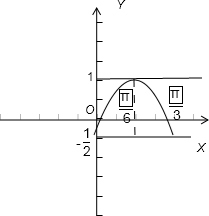
令f(x)=
•a
+b
=sin(4x-1 2
),g(x)=m,在同一直角坐标系中π 6
作出两个函数的图象,可知:m=1或m=-1 2