问题
计算题
如图所示，在质量为M的电动机上，装有质量为m的偏心轮，（偏心轮的重心距转轴r，偏心轮等效为用一长为r的细杆固定质量为m（轮的质量）的质点，绕转轴转动。）轮匀速转动，当轮重心在转轴正上方时，电动机对地面的压力刚好为零。
求：（1）当轮重心在转轴正上方时，细杆的作用力多大？
（2）轮转动的角速度ω多大?
（3）当轮重心在转轴正下方时，细杆的作用力多大？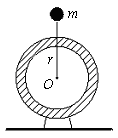
答案
（1）F=Mg（2）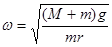
（3）（M＋2m）g
（1）轮的重心在正上方时，电动机对地面的压力刚好为零，则此时偏心轮对电动机向上的作用力大小等于电动机的重力。即F=Mg 2分 ①
（2）根据牛顿第三定律，此时轴对偏心轮的作用力向下，大小为F=Mg，其向心力为
F＋mg=mω2r 3分 ②
由①②得偏心轮重心到转轴的距离为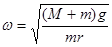： 2分③
（3）当偏心轮的重心转到最低点时，电动机对地面的压力最大.对偏心轮有
F′－mg=mω2r 3分 ④
由③、④、⑤解得F′=（M＋2m）g 2分
电动机对地面的压力刚好为零，说明杆对电动机的拉力等于电动机的重力，再以m为研究对象，拉力和重力的合力提供向心力，列式求解