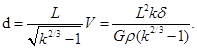如图所示,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油.假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原竖直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.
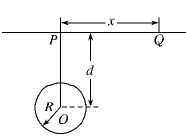
(1)设球形空腔体积为V,球心深度为d(远小于地球半径),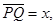 求空腔所引起的Q点处的重力加速度反常;
求空腔所引起的Q点处的重力加速度反常;
(2)若在水平地面上半径为L的范围内发现:重力加速度反常值在δ与kδ(k>1)之间变化,且重力加速度反常的最大值出现在半径为L的范围的中心.如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积.
(1) 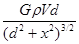 (2)
(2) 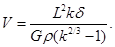
(1)如果将近地表的球形空腔填满密度为ρ的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常可通过填充后的球形区域产生的附加引力
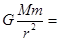 mΔg①
mΔg①
来计算,式中m是Q点处某质点的质量,M是填充后球形区域的质量.
M=ρV②
而r是球形空腔中心O至Q点的距离
r=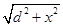 ③
③
Δg在数值上等于由于存在球形空腔所引起的Q点处重力加速度改变的大小。Q点处重力加速度改变的方向沿OQ方向,重力加速度反常Δg′是这一改变在竖直方向上的投影
Δg′=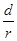 Δg④
Δg④
联立①②③④式得
Δg′=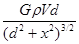 ⑤
⑤
(2)由⑤式得,重力加速度反常Δg′的最大值和最小值分别为
(Δg′)max=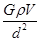 ⑥
⑥
(Δg′)min=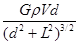 ⑦
⑦
由题设有
(Δg′)max=kδ,(Δg′)min=δ⑧
联立⑥⑦⑧式得,地下球形空腔球心的深度和空腔的体积分别为