arcsin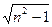

细光束从一腰入射后的折射角和从另一腰出射时的入射角之和为90°，而后者恰好为临界角时，前者的入射角最大。

设入射时的入射角为i₁，折射角为r，出射时的入射角为i₂，且i₂等于临界角，r+i₂=90°。

根据折射定律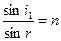,sinr=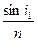,sini₂=,

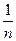sin²r+sin²i₂=，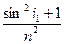

即sin²(90°-i₂)+sin²i₂=，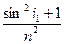

由于sin(90°-i₂)=cosi₂。

则sin²i₁+1=n²，

sini₁=。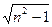

入射角最大值为arcsin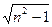。