问题
填空题
已知函数f(x)=
|
答案
∵f(x)=
=x-1 x-2
=1+x-2+1 x-2
,1 x-2 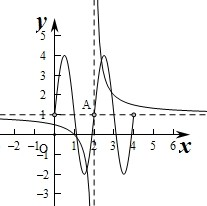
∴函数f(x)关于点(2,1)对称.
∵函数y=3sinπx关于点(2,0)对称,
∴g(x)=3sinπx+1(0<x<4)也关于点(2,1)对称,
作出函数f(x)和g(x)的图象,可以y=f(x)与y=g(x)的图象有四个交点,
它们彼此都关于点(2,1)对称,
设关于对称的两个点的横坐标分别为a,b和c,d,
则
=2,a+b 2
=2,c+d 2
即a+b=4,c+d=4,
∴a+b+c+d=4+4=8,
故答案为:8.
