问题
解答题
已知二次函数f(x)和一次函数g(x)的图象都经过原点,且f(x+1)=f(x)+2x,g(x)-g(x-1)=
(1)求f(x)和g(x)的解析式; (2)解关于x的不等式:f(x)<
|
答案
(1)∵二次函数f(x)和一次函数g(x)的图象都经过原点,
∴设二次函数f(x)=ax2+bx(a≠0)
又∵f(x+1)=f(x)+2x,
即a(x+1)2+b(x+1)=ax2+bx+2x
即2ax+a+b=2x
解得a=1,b=-1
故f(x)=x2-x
设一次函数g(x)=kx(k≠0)
∵g(x)-g(x-1)=
.1 4
∴kx-k(x-1)=1 4
即k=1 4
故g(x)=
x1 4
(2)不等式:f(x)<
.1 g(x)
可化为x2-x<4 x
即
<0x(x2-x)-4 x
即
<0x3-x2-4 x
即x(x3-x2-4)<0
即x(x-2)(x2+x+2)<0
解得0<x<2
故关于x的不等式:f(x)<
解集为(0,2)1 g(x)

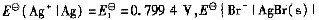 Ag=
Ag=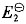 =0.0711V。试求25℃时,AgBr(s)在纯水中的溶度积Ksp为()。
=0.0711V。试求25℃时,AgBr(s)在纯水中的溶度积Ksp为()。