∵函数f（x）=

1

3

x³-2x²+3x-2，∴f^′（x）=x²-4x+3=（x-1）（x-3），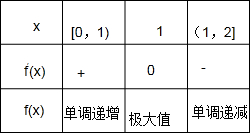

令f^′（x）=0，又x∈[0，2]，解得x=1．

列表如下：

由表格可知：当x=1时，f（x）取得极大值，也即最大值，f（1）=

1

3

-2+3-2=-

2

3

．

由f（0）=-2，f（2）=

1

3

×23-2×22+3×2-2=-

4

3

．

∴f（0）＜f（2）．

利用表格可知：最小值为f（0）．

∴函数f（x）在区间[0，2]上最大值与最小值的和=f（1）+f（0）=-

2

3

-2=-

8

3

．

故答案为-

8

3

．