问题
问答题
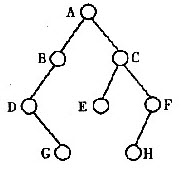
已知一棵二叉树的前序遍历序列是ABDGCEFH,其中序遍历序列为DGBAECHF。请画出相应的二叉树,并求出对应此二叉树的后序遍历序列,此二叉树是完全二叉树吗完全二叉树有什么性质(特点)
答案
参考答案:
根据二叉树的遍历规则,前序遍历总是先访问根结点,然后依次遍历其左右子树,而中序遍历规则是先遍历左子树,再访问根结点,然后访问右子树,则由以上规则,我们极易得出此二叉树的根结点是A,中序遍历序列中,根结点左右两边的结果分别属于其左、右子树,所以得出左子树包含3个节点:B,D,G,右子树包含四个结点C,E,F,H。在左子树中,先序遍历序B位于最前,而中序遍历序列中,B位于最后,则可以得出结点B无右子树,只有左子树,又在B的子树中,无论先序遍历还是中序遍历,D都位于G的前面,则G只能是D的右孩子,且D无左孩子,按照以上分析规则,我们同样可以分析出此二叉树的右子树的结构。从而我们得到了此二叉树的最终结构为: 此二叉树的后序遍历序列为:GDBEHFCA 从求出的二叉树的形状我们可以看出此二叉树不是完全二叉树,完全二叉树的性质是:一棵完全二叉树只有最下面的两层的结点数可以小于2,并且最下面一层的结点都集中在该层最左边的若干位置上。