问题
单项选择题
过原点作曲线y=ex的切线,则切线的方程为()
A.y=ex
B. y=ex
C. y=x
D.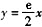
答案
参考答案:B
解析:
本题中f(x)=ex f′(x)=ex设所求切线方程为y-ex0=ex0(x-x0)由于切线过原点,所以0-ex0=ex0(0-x0)解得x0=1故所求切线方程为,y-e=e(x-1)即y=ex,答案选B。
过原点作曲线y=ex的切线,则切线的方程为()
A.y=ex
B. y=ex
C. y=x
D.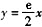
参考答案:B
解析:
本题中f(x)=ex f′(x)=ex设所求切线方程为y-ex0=ex0(x-x0)由于切线过原点,所以0-ex0=ex0(0-x0)解得x0=1故所求切线方程为,y-e=e(x-1)即y=ex,答案选B。