（I）∵当x＜0时，f（x）=x²+2x，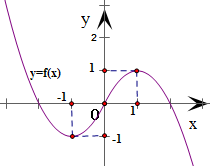

∴当x＞0时，f（-x）=（-x）²+2（-x）=x²-2x，

∵f（x）是定义在R上的奇函数，

∴f（0）=0，且当x＞0时f（x）=-f（-x）=2x-x²，

因此，函数f（x）的解析式为f(x)=

-x2+2x，(x＞0) 0，(x=0) x2+2x，(x＜0)

；

（I）由（1）求出的f（x）解析式，作出f（x）的图象如图所示．

若f（x）在x∈[a，b]时，函数值的集合为[

1

b

，

1

a

]，

则a＜b且

1

b

＜

1

a

，可得a＜b＜0或0＜a＜b．

①当a＜b＜0时，若a∈（-1，0），则

1

a

＜-1．

由于函数f（x）在（-∞，0）的最小值为-1，所以不存在x∈[a，b]使函数值的集合为[

1

b

，

1

a

]，

因此a∈（-∞，-1]，同理可得b∈（-∞，-1]，

∴a＜b≤-1，可得f（x）在[a，b]上为减函数，

即

f(a)=a2+2a= 1 a f(b)=b2+2b= 1 b

，解之得

a=- 1+ 5 2 b=-1

；

②当0＜a＜b时，类似①的方法可得a∈[1，+∞），且b∈[1，+∞）．

∴1≤a＜b，可得f（x）在[a，b]上为减函数，

即

f(a)=a2+2a= 1 a f(b)=b2+2b= 1 b

，解之得

a=1 b= 1+ 5 2

．

综上所述，存在

a=1 b= 1+ 5 2

或

a=- 1+ 5 2 b=-1

，使得f（x）在x∈[a，b]时，函数值的集合为[

1

b

，

1

a

]．