函数f（x）=xx∈P-xx∈M其中P、M为实数集R的两个非空子集，又规定f（P

问题选择题

函数f（x）=

x	x∈P
-x	x∈M

其中P、M为实数集R的两个非空子集，又规定f（P）={y|y=f（x），x∈P}，f（M）={y|y=f（x），x∈M}．给出下列四个判断，其中正确判断有（　　）
①若P∩M=∅，则f（P）∩f（M）=∅；
②若P∩M≠∅，则f（P）∩f（M）≠∅；
③若P∪M=R，则f（P）∪f（M）=R；
④若P∪M≠R，则f（P）∪f（M）≠R．

A．1个

B．2个

C．3个

D．4个

答案

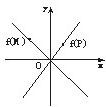
由题意知函数f（P）、f（M）的图象如图所示．

设P=[x₂，+∞），M=（-∞，x₁]，

∵|x₂|＜|x₁|，f（P）=[f（x₂），+∞），

f（M）=[f（x₁），+∞），则P∩M=∅．

而f（P）∩f（M）=[f（x₁），+∞）≠∅，故①错误．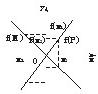

同理可知②正确．

设P=[x₁，+∞），M=（-∞，x₂]，

∵|x₂|＜|x₁|，则P∪M=R．

f（P）=[f（x₁），+∞），f（M）=[f（x₂），+∞），

f（P）∪f（M）=[f（x₁），+∞）≠R，

故③错误．

④由③的判断知，当P∪M≠R，则f（P）∪f（M）≠R是正确的．

故④对

故选B