问题
计算题
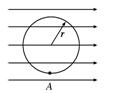
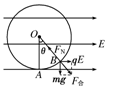
(14分)半径为r的绝缘光滑圆环固定在竖直平面内，环上套有一质量为m、带正电的珠子，空间存在水平向右的匀强电场，如图14所示．珠子所受静电力是其重力的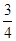
倍，将珠子从环上最低位置A点由静止释放，求：
(1)珠子所能获得的最大动能是多少？
(2)珠子对圆环的最大压力是多少？
答案
(1)
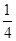mgr (2)
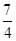mg
(1)设qE、mg的合力F合与竖直方向的夹角为θ，
因qE＝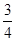
mg，所以tanθ＝
＝，
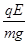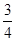则sinθ＝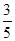
，cosθ＝
，
则珠子由A点静止释放后在从A到B的过程中做加速运动，如图所
示．由题意知珠子在B点的动能最大，由动能定理得
qErsinθ-mgr(1-cosθ)=Ek，
解得Ek=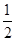
mgr.
(2)珠子在B点对圆环的压力最大，设珠子在B点受圆环的弹力为FN，则FN－F合＝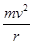
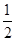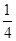(mv2＝mgr)
即FN＝F合＋＝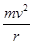
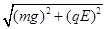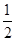＋mg
＝
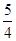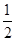mg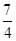＋mg＝mg.
由牛顿第三定律得，珠子对圆环的最大压力为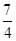mg.