问题
计算题
如图所示，在水平转台上放有A、B两个小物块，它们到轴心O的距离分别为rA="0.2" m,rB="0.5" m,它们与台面间静摩擦力的最大值为其重力的0.4倍，取g="10" m/s2。
(1)当转台转动时，要使两物块都不相对台面滑动，求转台角速度的最大值；
(2)当转台转动时，要使两物块都相对台面滑动，求转台转动的角速度应满足的条件；
(3)现保持A、B两个小物块位置不变，用水平轻杆将两物块连接， 已知mA=5 mB , mB="2" kg。当转台转动角速度为某一值时，两物块恰好对台面未发生相对滑动，求此状态下轻杆对物块B的弹力。
答案
(1) 
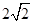rad/s (2) ω＞2
rad/s (3) F=8N 方向指向圆心
题目分析：(1)因为rB＞rA.所以B物块先滑动.
Ffm="0.4" mBg ① F向=mBωB2rB ②
当B恰不相对台面滑动时，应有F向=Ffm ③
联立①、②、③式解得0.4mBg=mBωB2rB ④解④式得ωB=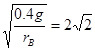
rad/s
(2)同理，当A恰不相对台面滑动时，应有0.4mAg=mAωA2rA,解得ωA=2 rad/s
故要使两物块都对台面发生滑动，ω的范围为ω＞2 rad/s(或取≥)。
(3) 设弹力大小为F，则0.4mAg—F= mAω2rA F+0.4mBg=mBω2rB
得ω="4" rad/s F=8N 方向指向圆心。
点评：注意本题中为静摩擦力与绳子的拉力充当向心力，故应注意静摩擦力是否已达到最大静摩擦力．