问题
计算题
如图所示，AB为竖直转轴，细绳AC和BC的结点C系一质量为m的小球，两绳能承担的最大拉力均为2mg。当AC和BC均拉直时∠ABC＝90°，∠ACB＝53°，BC＝1m。竖直轴AB匀速转动，C球在水平面内做匀速圆周运动。
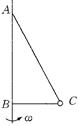
求：
（1）要使两条细绳都拉直，C球的线速度至少多大？
（2）当C球的线速度增大时，AC和BC哪条绳先断？当其中一条绳刚要断时，C球的线速度多大？
（g＝10m／s2，sin53°＝0.8，cos53°＝0.6）
答案
（1）
m／s（2）BC绳先断，
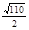m／s
题目分析：（1）若角速度太小，则BC绳子容易松弛，即dangBC刚好松弛，且未发生形变时，此时转速最小，即AC绳子拉力和重力提供向心力：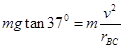
，代入数据则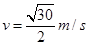
（2）C求速度继续增加，则AC、BC绳子拉力变大，只要绳子不断，即
，
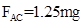，只要BC不断，AC就不会断。显然BC先断。即当BC刚好要断时、AC的拉力和重力，三个力提供向心力，
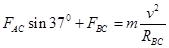此时，线速度为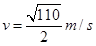
点评：本题考查了圆周运动临界问题的分析，通过向心力来源的分析判断临界条件。