问题
计算题
(18分)如图甲所示，直角坐标系中直线AB与横轴x夹角∠BAO=30°，AO长为a。假设在点A处有一放射源可沿∠BAO所夹范围内的各个方向放射出质量为m、速度大小均为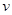
、带电量为e的电子，电子重力忽略不计。在三角形ABO内有垂直纸面向里的匀强磁场，当电子从顶点A沿AB方向射入磁场时，电子恰好从O点射出。试求：
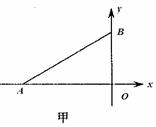
（1）从顶点A沿AB方向射入的电子在磁场中的运动时间t；
（2）速度大小为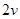
的电子从顶点A沿AB方向射入磁场（其它条件不变），求从磁场射出的位置坐标。
（3）磁场大小、方向保持不变，改变匀强磁场分布区域，使磁场存在于三角形ABO内的左侧，要使放射出的速度大小为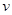电子穿过磁场后都垂直穿过y轴后向右运动，试求匀强磁场区域分布的最小面积S。（用阴影表示最小面积）
答案
（1） 
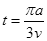(2) (0，
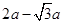) （3）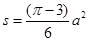
题目分析：（1）根据题意，电子在磁场中的运动的轨道半径R=a
由evB=mv2/a 得：B=mv/ea
由T=2πm/eB
t=T/6=πa/3v
(2)由evB=mv2/r，得r=" mv/eB" ，因此其它条件不变，当速度大小为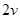
时，r=2a如图所示，从磁场射出的位置坐标为 (0，)
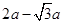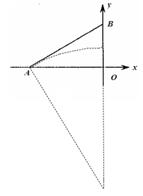
（3）有界磁场的上边界：沿AB方向发射的电子在磁场中运动轨迹与AO中垂线交点的左侧圆弧。有界磁场的下边界：以A点的正上方、距A点的距离为a的点为圆心，以a为半径的圆弧。如图所示：
最小面积为：