问题
选择题
半径R=4cm的圆盘可绕圆心O水平转动，其边缘有一质量m=1kg的小物块（可视为质点），若物块随圆盘一起从静止开始加速转动，其向心加速度与时间满足a0=t2，物块与圆盘间的动摩擦因数为0.6，则：
A．2s末圆盘的线速度大小为0.4m/s
B．2s末物块所受摩擦力大小为4N
C．物块绕完第一圈的时间约为1.88s
D．物块随圆盘一起运动的最大速度约为0.5m/s
答案
ABD
题目分析: 物块随圆盘做匀速圆周运动，由静摩擦力提供向心力，2S末圆盘的向心加速度a=4m/s2，根据a=ω2r，解得ω=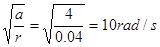
，2S末圆盘的线速度大小v=rω=0.4m/s，故A正确；由牛顿第二定律，2S末物块所受摩擦力大小Ff=ma=4N，故B正确；向心加速度与时间满足a0=t2，所以角速度与时间满足ω=
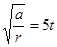。所以物块绕完第一圈平均角速度
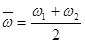=5rad/s，所以物块绕完第一圈的时间t=
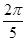=1.25s，故C正确；物块随圆盘一起运动的最大速度时，静摩擦力是最大静摩擦力，μmg=
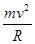，解得：v=
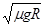=0.49m/s，约为0.5m/s，所以D正确；