问题
计算题
如图所示,有一长为L的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直面内做完整的圆周运动。已知水平地面上的C点位于O点正下方,且到O点的距离为1.9L。不计空气阻力。求:
(1)小球通过最高点A时的速度vA;
(2)小球通过最低点B时,细线对小球的拉力T;
(3)若小球运动到最低点B时细线恰好断裂,小球落地点到C点的距离。

答案
解:(1)小球恰好能做完整的圆周运动,则小球通过A点时细线的拉力为零,根据向心力公式有: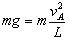
解得: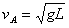
(2)小球从A点运动到B点,由机械能守恒定律有: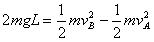
解得: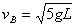
小球在B点时根据牛顿第二定律有: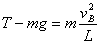
解得:T=6mg
(3)小球运动到B点时细线断裂,小球做平抛运动,有: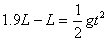
x=vBt=3L
