问题
计算题
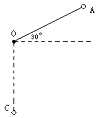
如图所示,一根不可伸长的轻质细线,一端固定于O点,另一端栓有一质量为m的小球,可在竖直平面内绕O点摆动,现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时,细线承受的拉力是多大?
答案
解:小球在松开后作自由落体运动,根据对称性,到达OA下方30°时自由落体结束。
设绳长L,则下落了L(等边三角形),
根据动能定理:1/2mv2=mgL
v=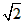 gL
gL
此后绳子被绷紧,作圆周运动。
但要注意的是这时圆周运动初速度不是v,而是v1=vcos30°
在开始圆周运动后,机械能守恒。
小球之后竖直方向下落L/2,则 1/2mv12+mgL/2=1/2mv22
v2=
又由圆周运动公式,绳子拉力F提供向心力 F=mv22/R
代入数据 F=7/2mgL/L=3.5mg。
