问题
解答题
某校拟派一名跳高运动员参加一项校陆比赛，对甲、乙两名跳高运动员进行了8次选拔赛，他们的成绩如下（单位：m）：
甲：1.70，1.65，1.68，1.69，1.72，1.73，1.68，1.67；
乙：1.60，1.73，1.72，1.61，1.62，1.71，1.70，1.75．
求： （1）甲的极差是 ，乙的极差是 ．
（2）你认为 的成绩比较稳定．
（3）经预测，跳高1.65m就很可能获得冠军，你认为应选 参加比赛．
答案
解：（1）甲的极差为：1.73﹣1.65=0.08；
乙的极差为：1.75﹣1.60=0.15；
（2）
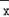甲=
（1.70+1.65+1.68+1.69+1.72+1.73+1.68+1.67）=
×13.52=1.69
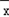乙=
（1.60+1.73+1.72+1.61+1.62+1.71+1.70+1.75）=
×13.44=1.68
s甲2=
[（1.70﹣1.69）2+（1.65﹣1.69）2+…+（1.67﹣1.69）2]=0.000 6
s乙2=
[（1.60﹣1.68）2+（1.73﹣1.68）2+…+（1.75﹣1.68）2]=0.003 15
∵s甲2＜s乙2，
∴甲的成绩比乙的成绩稳定．
（3）该校要获取跳高比赛冠军应选甲参加比赛，因为甲的跳高成绩8次都不低于1.65m，而乙只有5次超过1.65m．
