问题
计算题
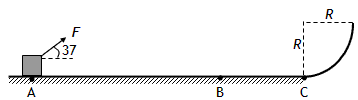
如图，粗糙水平面与半径R=2m的光滑圆弧轨道相切于C点。静止于A处的物体，在大小为10N、方向与水平面成37°角的拉力F作用下沿水平面运动，到达C点时立即撤去F，物体沿光滑圆弧向上冲，然后返回经过C点进入水平面且停在B处。已知：物体返回经过C点时对轨道压力大小为物体重量的2.8倍，sAC=15m，sBC=4.5m，取g=10m/s2，sin37°=0.6，cos37°=0.8．求：
（1）物体的质量；
（2）物体与水平面的动摩擦因素。
答案
解：（1）设物体的质量为m，与水平面的动摩擦因数为μ，经过C点时的速度为vC。
物体返回经过C点时，由牛顿第二定律：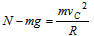
①
依题意：
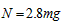②
联立①②并代入R=2m，g=10m/s2，得：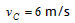
③
从C到B，动能定理：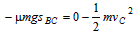
④
由③④并代入sBC=4.5m，g=10m/s2，解得：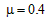
⑤
（2）由于圆弧轨道光滑，物体第一次通过C与第二次通过时的速度大小相等。
A到C，由动能定理：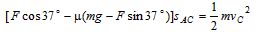
⑥
由③⑤⑥并代入F=10N，sAC=15m，g=10m/s2，解得：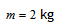
。